معرفیکامل و دقیق از روش معروف حل مسئله ریاضی پولیا.
به طور کلی، در تحقیقات مختلف دوهدف اصلی براي آموزش ریاضی در نظر گرفته اند. اولین هدف كه ایدهاي خوب،ولی محدود به حساب میآید،كسب توانایی براي انجام دادن محاسبات است.
برخی از افراد، این هدف رابهکارگیری یا كاربردریاضیات تعبیرکردهاند. هدف دوم كه اساسیتر و ارزشمندتر به نظر میرسد، پرورش تفکر است. حل مسئلهیکی ازبهترین راههای پرورش تفکر ریاضی به حساب میآید.
اگر بخواهیم یک تعریف ساده از مسئله داشته باشیم میتوان گفت:
مسئله را همان روش روبهروشدن با چالشی دانست كه راهبرد یا راهکار از پیش آمادهای براي حل آن وجود ندارد.
آقای پولیا معتقد است که مسئله میتواند پیچیده یا ساده باشد. درحالت اول،پیداكردن راهحل آن دشوار و درحالت دوم آسان است. در ضمن دشواري راهحل تاحد زیادي به خود مفهوم مسئله مربوط میشود. چراکه میگویند:آنجا كه دشواري نباشد ، مسئلهای وجود ندارد.
معرفی دقیق چارچوب حل مسئله ریاضی پولیا
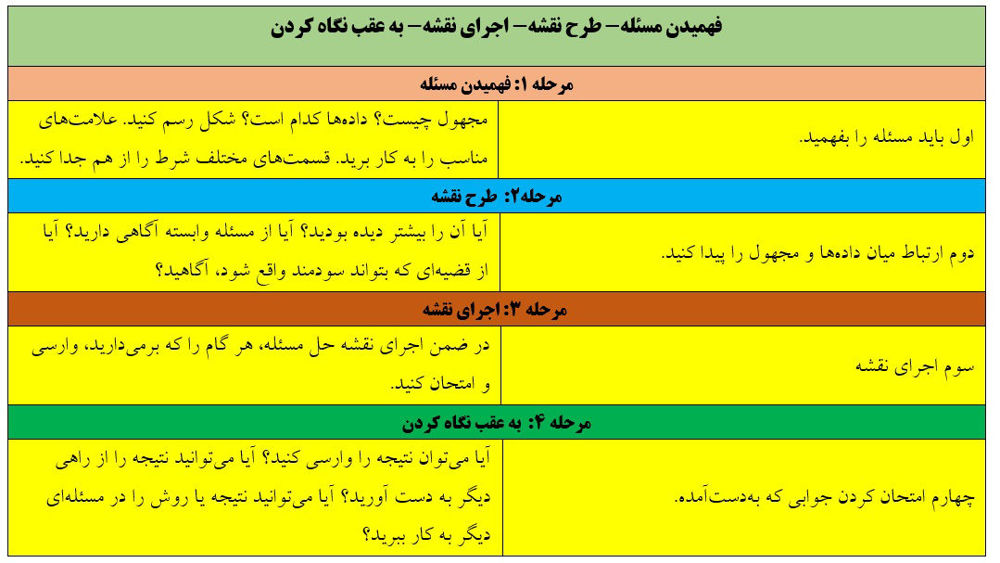
پولیا ، پس از سالها تلاش و پژوهش در حوزه ریاضیات، چارچوب خود را برای حل مسئله ریاضی ارائه کرد. این مدل 4 مرحلهای عبارتاند از:
- فهمیدن مسئله
- طرح نقشه
- اجرای نقشه
- بازگشت به عقب
پولیا یک ریاضی دان بود و با حل مسئله ، و عقب و جلو رفتنها برای حل یک مسئله آشنا بود . با این وجود ، این چهار مرحله خطی هستند . پولیا کتابش را برای خوانندگان ، دانش آموزان و معلمان علاقهمند نوشته است و نه برای محققان . دنبال کردن مراحل خطی آسانتر است تا روشهای پیچیده . اگر چه پولیا کار خود را برای معلمانی که مایل هستند توانایی دانش آموزان خود را برای حل مسئله ( و همچنین دانشآموزانی که علاقه دارند تواناییهای خویش را برای حل مسائل ) توسعه دهند ؛ نوشته است ، اما مراحل او به عنوان یک چارچوب برای حل مسئله ، توسط محققان رشتههای مختلف استفاده شده است .
او پس از کار با دانشجویان و بازتاب دادن تلاش آنها برای حل مسائل ریاضی ، چارچوب خود و سؤالات و دستورالعملهایی را برای هر یک از این مراحل برای کمک به حل مسئله و به دست آوردن راهحل ارائه داد.
پولیا ، تسلط بر ریاضیات و توانایی و مهارت در حل مسئله را به معنای داشتن استقلال اندیشه ، عقل سلیم و نیروی نوآفرینی دانسته است . بهاینترتیب ، نخستین و مهمترین وظیفهی ریاضیات دورهی دبیرستانی ، تأکید بر جنبههای منطقی متکی بر روش حل مسئله است . از طرفی ، حل یک مسئله، ضرورتاً با به دست آوردن پاسخ صحیح کامل نمیشود . یک مسئله بهراستی حلنشده است مگر اینکه یادگیرنده بفهمد ، که چه کرده است و بداند چرا آن کارها مناسب بوده است .
گام اول ، فهمیدن مسئله ،با شناسایی چیزی آغاز میشود که توسط مسئله مطرح شده است ؛ یعنی حل کننده مسئله باید ماهیت سؤال پرسیده شده را درک کند . برای این منظور مهم است که همهی دادههای موجود در مسئله را تشخیص دهیم و شرایط لازم و کافی ، مرتبط ، اضافی و متناقض را در میان اطلاعات داده شده ، تعیین کنیم . حقایق و اطلاعات بیشتری ممکن است از رسم نمودارهای مناسب و یا معرفی نمادهای مناسب ، به دست آیند .
گام دوم طرح نقشه است .نقشهای که بهخوبی طراحی شده ، شرایط یک ارتباط ساده بین دادهها و مجهولها را فراهم میکند. علاوه بر این، تجربیات حل مسائل در گذشته نیز در این مرحله حائز اهمیت است .
بنابراین مهم است که مسائل مشابهی را در نظر بگیریم ،که برخی از آنها ممکن است در ظاهر از منظر مسئلهی تحت بررسی، متفاوت باشند. تکنیکهای خاص و نتایجی که در طول حل مسئله گذشته مورد استفاده قرارگرفتهاند، ممکن است یک تعریف مجدد از ارائه کنند. پولیا بسیاری از راهبردها را برای حل مسائل ریاضی مورد بحث قرار داده است، از جمله رسم شکل، حل مسئلهی سادهتر، مسائل مشابه توجه به موارد خاص برای پیدا کردن الگوهای عمومی، برگشت به عقب و به کارگیری دیدگاههای مختلف.
در ادامه این مطلب از موسسه عصر دانش و حافظه فهرستی از رهیافت های (راهبردهای) حل مسئله ارائه شدهاند :
- تغییر دیدگاه
- کار روی مسائل کمکی
- حل مسئله معادل
- کار به عقب
- در نظر گرفتن تمام حالتها (اشباع)
- حل یک معادله
- جستجوی فرمول
- شبیهسازی انجام دهید
- از یک مدل استفاده کنید
- دنبال کردن زوجیت
- شناسایی زیر اهداف
- استفاده از محورهای مختصات
- استفاده از تقارن
- زیر مسئله
- تعیین چیزهایی که میدانید و چیزهایی که سعی میکنید، پیدا کنید.
- حدس و آزمایش
- رسم شکل
- استفاده از متغیر(بهکارگیری نماد کارآمد)
- جستجوی الگو
- تهیه لیست (جدول نظامدار)
- حل مسئلهی سادهتر (اعداد کوچکتر- موارد خاص- شرایط خاص - متغیرهای کمتر )
- رسم نمودار
- استفاده از استدلال مستقیم
- استفاده از استدلال غیرمستقیم
- استفاده از خواص اعداد
- عمل قهقرایی
- راهحل بازگشتی
- حذف حالتهای نامطلوب
- مسئله را حلشده فرض کنید
گام سوم پولیا این است که نقشه را اجرا کنیم.مهم است که هر مرحله از نقشه را با دقت اجرا کنیم و بررسی کنیم که هر مرحله، به صورت منطقی دنبال شده است. باید توجه داشت که طرح نقشه و اجرای آن دو موضوع متفاوتاند. به طور طبیعی، ممکن است موانع و دشواریهای زیادی بر سر راه اجرای نقشه وجود داشتهباشد.
گام چهارم"بازگشت به عقب" است. پیدا کردن یک راهحل، به حتم به این معنا نیست که روند حل مسئله به پایان رسیده است.
حال که این چهار مرحله را با دقت مرور کردیم میتوان گفت:
در بخش اول از مرحلهی چهارم پولیا، حل کننده مسئله، راه حل به دست آمده را از طریق چک کردن استدلالهای موجود در مسیر و تأیید عدم وجود اشتباه در استدلالها بررسی میکند.
در بخش دوم از مرحله چهارم پولیا،حلکننده مسئله، یافتن راههای جایگزین برای حل مسئله مشابه را بررسی میکند. استخراج نتیجه بهدستآمده از طریق استفاده از رویکردهای جایگزین میتواند برای حل مسئله در آینده مفید باشد.
پولیا زمان بسیار زیادی را برای نشان دادن چارچوب خود از حل مسئله با نمونههای عینی اختصاص داده است.در نتیجه، این چارچوب، علاقهی مخاطبان بسیاری را به دست آورده است. او خوانندگان خود را متقاعد کرد که فرآیندهای حل مسئلهای که او آنها را تحلیل کرده است، نه تنها برای ریاضی دانان قابل دسترسی هستند، بلکه میتوانند توسط مخاطبان گستردهتری استفاده شوند.
بسیاری از محققان در آموزش ریاضی، چارچوب پولیا را به صورت جامع و نظاممند موردبررسی قرار داده اند. مرور ادبیات پیشین نشان میدهد که بخش زیادی از این توجه به طور خاص در سه مرحلهی اول متمرکز شده اند. در واقع، بسیاری محققان به طور خاص، جذب مرحلهی دوم شده اند یعنی طراحی یک نقشه، زیرا این چیزی است که اکثر معلمان در کلاس درس به دانشآموز خود در یادگیری ریاضیات آموزش می دهند. با این وجود، چارچوب حل مسئلهی پولیا در مرحلهی سوم به پایان نمیرسد. فقط تعدد محدودی از مطالعات در ریاضیات، استفاده از رویکردهای جایگزین در حل مسئله را بررسی کرده اند.
با وجود اهمیت آن، چهارمین مرحلهی پولیا در جامعه آموزش ریاضی کمتر از سه مرحلهی دیگر از دیدگاه تجربی، مورد توجه قرار گرفته است.
برخی از محققان در این زمینه، به ویژه در استفاده از تکالیف ریاضی که دانش آموزان را ملزم به حل یک مسئله از طریق چندین راهحل مختلف میکند؛ موفق بودهاند. این محققان، حضور مفاهیم ریاضی مختلف را از طریق حل مسائل غیرمعمولی به کمک راهحلهای چندگانه، از طریق تبدیل مسائل استاندارد به مسائل غیراستاندارد و یا از طریق شناسایی ویژگیهای خاص در مسائل استاندارد بررسی کردهاند.
چارچوب پولیا برای فرایند حل مسئله [برگرفته از کتاب حل مسئله ریاضی، از نظریه تا عمل، دکتر ابراهیم ریحانی]
منبع:
1- کتاب حل مسئله ریاضی، از نظریه تا عمل، دکتر ابراهیم ریحانی، سعیدحقجو
2- کتاب حل مسئله در ریاضی، جلد دوم. (معرفی راهبردهای حل مسئله ویژه دانشآموزان پایه سوم تا هفتم)، نویسندگان: آقای دکتر جلیل پاکدامن، خانم دکتر نغمه توسلی
